Curve fitting

Wersja pdf

“Curve fitting” (dopasowanie krzywej) to zadanie sprowadzająca się do szukania najbardziej dopasowanego modelu.

W przykładach ograniczymy się do jednej zmiennej objaśniającej, jednak można to w dosyć prosty sposób zastosować również przy kilku zmiennych objaśniających.

x <- c(32,64,96,118,126,144,152.5,158)
y <- c(99.5,104.8,108.5,100,86,64,35.3,15)
plot(x,y, pch=20)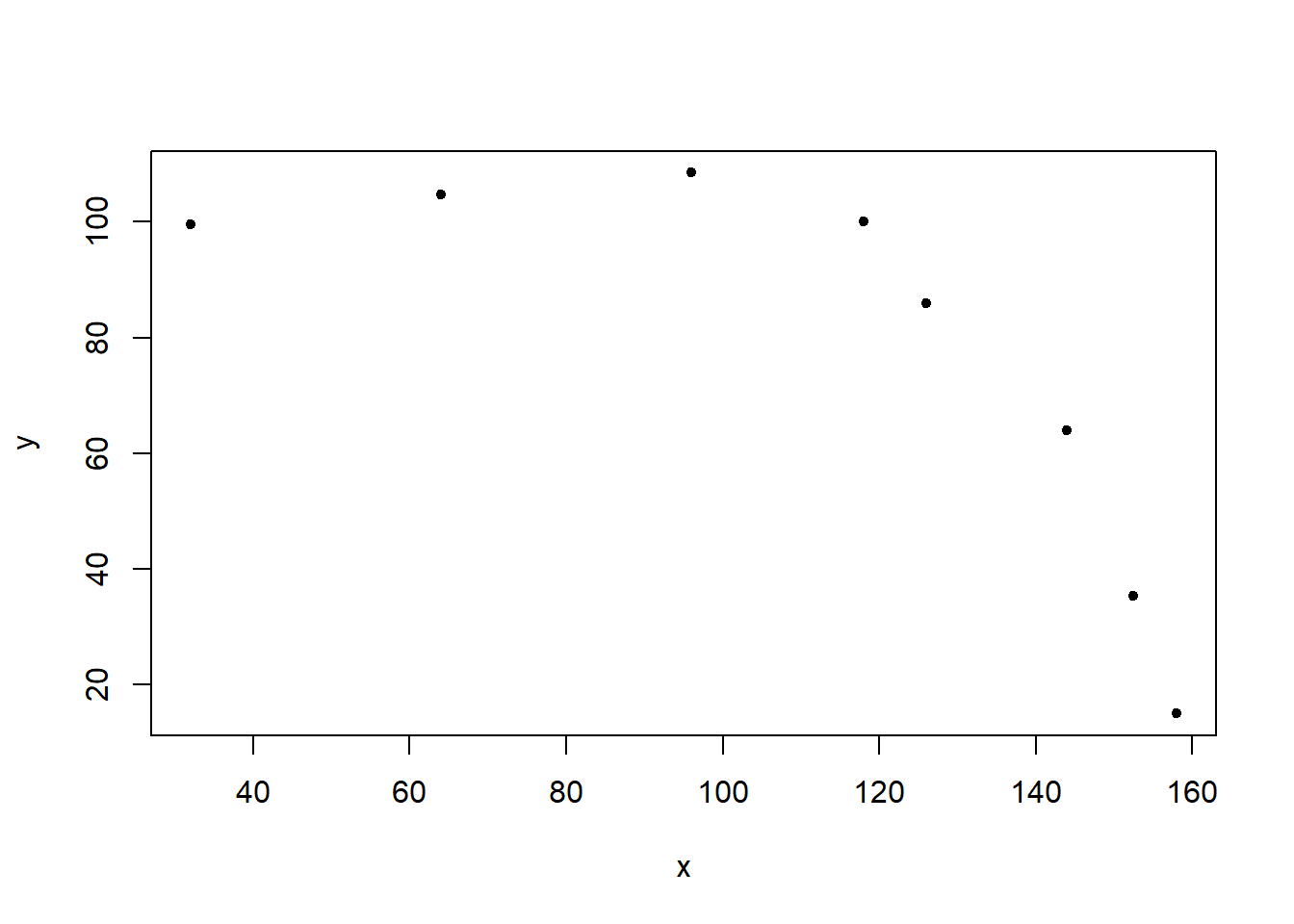

Stwórzmy kilka modeli i zrób wykresy teoretycznych wartości z modelu:

model1  <- lm(y~x)
model2 <- lm(y~poly(x,2,raw=TRUE))
model3 <- lm(y~poly(x,3,raw=TRUE))
model4 <- lm(y~poly(x,4,raw=TRUE))
x.axis <- seq(30,160, length=50)
plot(x,y,pch=20,ylim=c(0,150))
lines(x.axis, predict(model1,data.frame(x=x.axis)), col="red")
lines(x.axis, predict(model2,data.frame(x=x.axis)), col="green")
lines(x.axis, predict(model3,data.frame(x=x.axis)), col="blue")
lines(x.axis, predict(model4,data.frame(x=x.axis)), col="purple")

Sprawdźmy \(R^2\):

summary(model1)$r.squared

## [1] 0.5759157

summary(model2)$r.squared

## [1] 0.9473663

summary(model3)$r.squared

## [1] 0.9923689

summary(model4)$r.squared

## [1] 0.9943288

Sprawdźmy skorygowane \(\overline{R}^2\):

summary(model1)$adj.r.squared

## [1] 0.505235

summary(model2)$adj.r.squared

## [1] 0.9263129

summary(model3)$adj.r.squared

## [1] 0.9866455

summary(model4)$adj.r.squared

## [1] 0.9867671

Co nam pokaże anova?

anova(model1,model2,model4,model3)

## Analysis of Variance Table
## 
## Model 1: y ~ x
## Model 2: y ~ poly(x, 2, raw = TRUE)
## Model 3: y ~ poly(x, 4, raw = TRUE)
## Model 4: y ~ poly(x, 3, raw = TRUE)
##   Res.Df    RSS Df Sum of Sq        F    Pr(>F)    
## 1      6 3660.8                                    
## 2      5  454.3  1    3206.4 196.4919 0.0007862 ***
## 3      3   49.0  2     405.4  12.4212 0.0353688 *  
## 4      4   65.9 -1     -16.9   1.0368 0.3835381    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Dodajmy model nieliniowy.

model5<-nls(y~poly(x,5,raw=TRUE)%*% coef, start = list(coef = c(a = 1, b = 2, c=2, d=4, e=2)))
anova(model4,model5)

## Warning in anova.lmlist(object, ...): models with response '"NULL"' removed
## because response differs from model 1

## Analysis of Variance Table
## 
## Response: y
##                        Df Sum Sq Mean Sq F value   Pr(>F)   
## poly(x, 4, raw = TRUE)  4 8583.2 2145.81   131.5 0.001064 **
## Residuals               3   49.0   16.32                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Musimy porównywać w większości wypadkóW modele “tego samego typu”:

model6<-nls(y~poly(x,4,raw=TRUE)%*% coef, start = list(coef = c(a = 1, b = 2, c=2, d=1)))
anova(model6, model5)

## Analysis of Variance Table
## 
## Model 1: y ~ poly(x, 4, raw = TRUE) %*% coef
## Model 2: y ~ poly(x, 5, raw = TRUE) %*% coef
##   Res.Df Res.Sum Sq Df Sum Sq F value Pr(>F)
## 1      4     79.383                         
## 2      3     60.188  1 19.195  0.9568 0.4001

Jak zatem porównywać? Pierwsza opcja to ręczne liczenie \(R^2\).

ym<-mean(y)
yh<-fitted(model4)
ssm<-sum((yh-ym)^2)
sst<-sum((y-ym)^2)
r2<-ssm/sst
r2

## [1] 0.9943288

yh<-fitted(model5)
ssm<-sum((yh-ym)^2)
sst<-sum((y-ym)^2)
r2<-ssm/sst
r2

## [1] 0.9946821

yh<-fitted(model6)
ssm<-sum((yh-ym)^2)
sst<-sum((y-ym)^2)
r2<-ssm/sst
r2

## [1] 0.998033

Zobaczmy wykresy.

plot(x,y,pch=20,ylim=c(0,150))
lines(x.axis, predict(model4,data.frame(x=x.axis)), col="red")
lines(x.axis, predict(model5,data.frame(x=x.axis)), col="blue")
lines(x.axis, predict(model6,data.frame(x=x.axis)), col="green")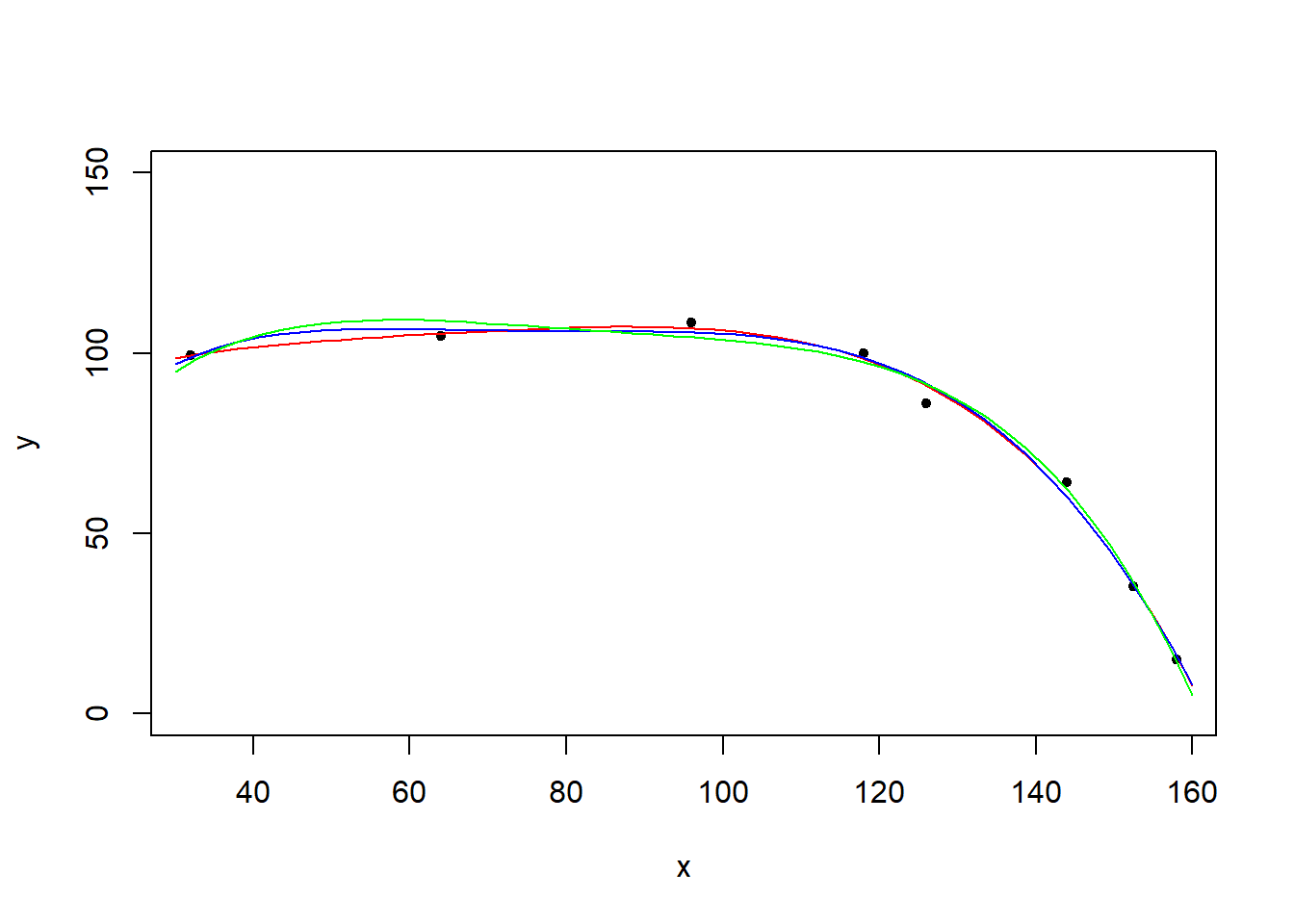

Jak to mierzyć? Możemy sprawdzić tzw. kryterium informacyjne Akaikego (Akaike Information Criterion) - link.

AIC(model1)

## [1] 77.71092

AIC(model2)

## [1] 63.01831

AIC(model3)

## [1] 49.56936

AIC(model4)

## [1] 49.19471

AIC(model5)

## [1] 50.84723

AIC(model6)

## [1] 51.06176

x<-seq(10,50,1)
y<-100/x+rnorm(1,sd=2)