Dzień 1 - Model liniowy - grafika
Model liniowy - grafika
Wersja pdf Uwaga: w pdf niektóre rysunki są źle rozmieszczone.
Załadujmy w R jak poprzednio:
library(tidyverse)
devtools::install_github("kassambara/datarium")
data("marketing", package = "datarium")
model <- lm(sales ~ youtube + facebook + newspaper, data = marketing)plot(model)



Wykres 1
Przeanalizujmy pierwszy wykres:
plot(model, which = 1)
Ręcznie możemy to uzyskać:
plot(model$fitted.values, model$residuals, ylab = "Residuals", xlab = "Fitted values", )
lines(lowess(model$fitted.values, model$residuals), col='red', lwd=2)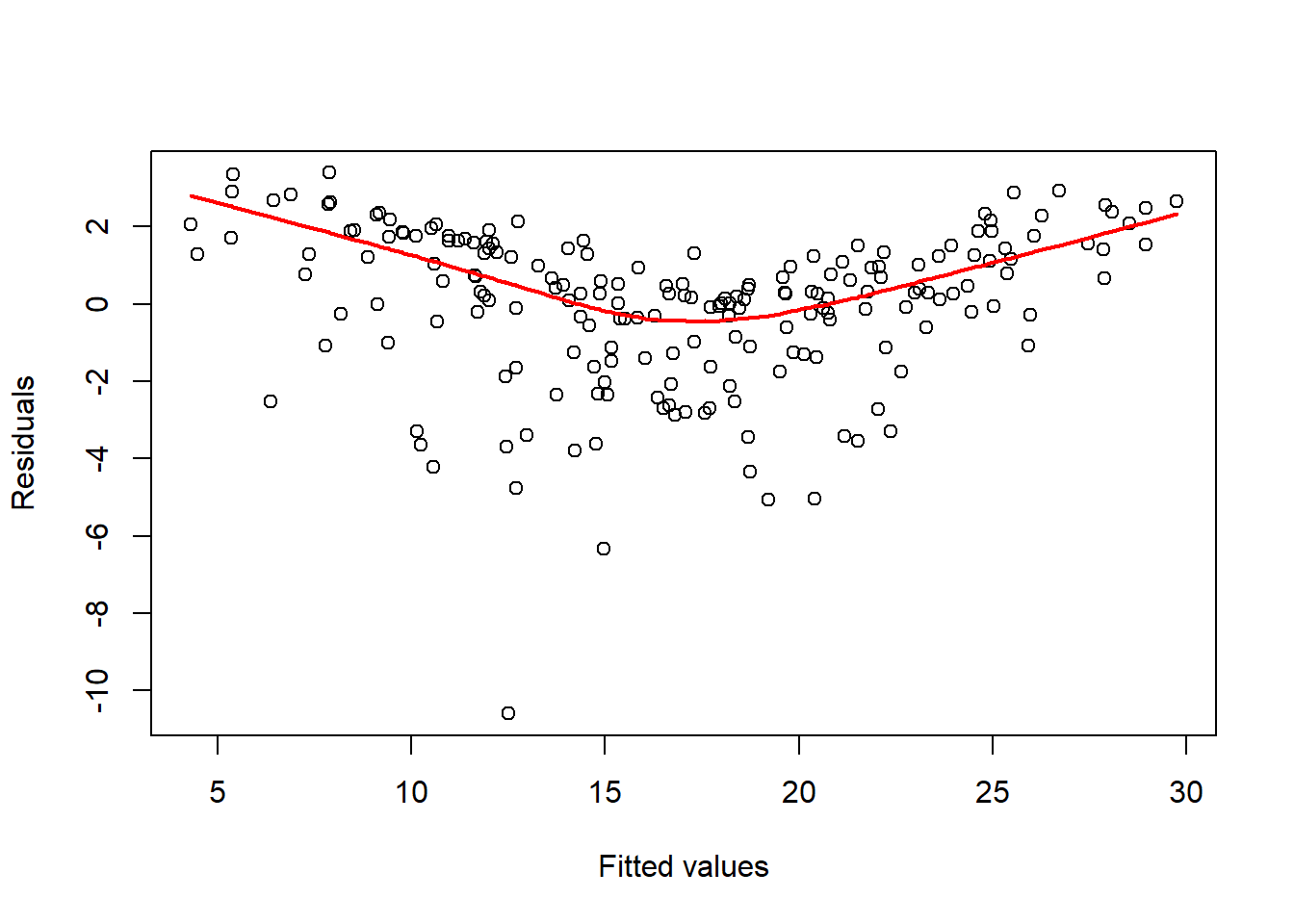
Wyjaśnienie na rysunku:
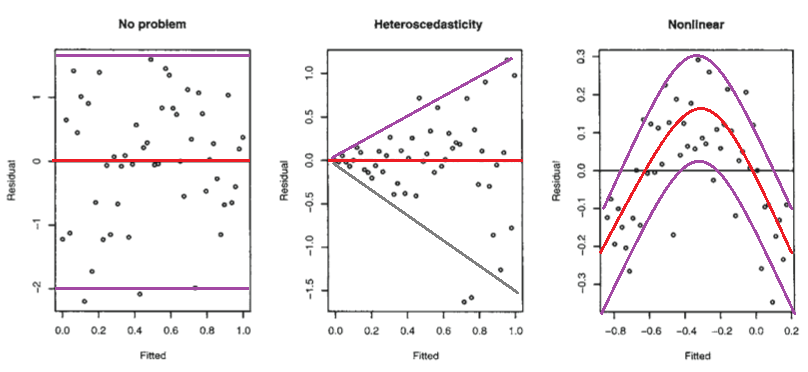
źródło zdjęcia: https://stats.stackexchange.com/questions/76226/interpreting-the-residuals-vs-fitted-values-plot-for-verifying-the-assumptions
Wykres 2
plot(model, which = 2)
Wykres Q-Q (kwantylowo-kwantylowy) informuje, na ile dopasowanie odbiega od rozkładu normalnego.
Wykres 3
plot(model, which = 3)
Ten wykres pokazuje, czy reszty są równomiernie rozłożone wzdłuż zakresów dopasowanych wartości. W ten sposób można sprawdzić założenie równej wariancji (homoscedastyczność). To dobrze, jeśli jest linia pozioma z równomiernie umieszczonymi punktami.
Wykres 5
plot(model, which = 5)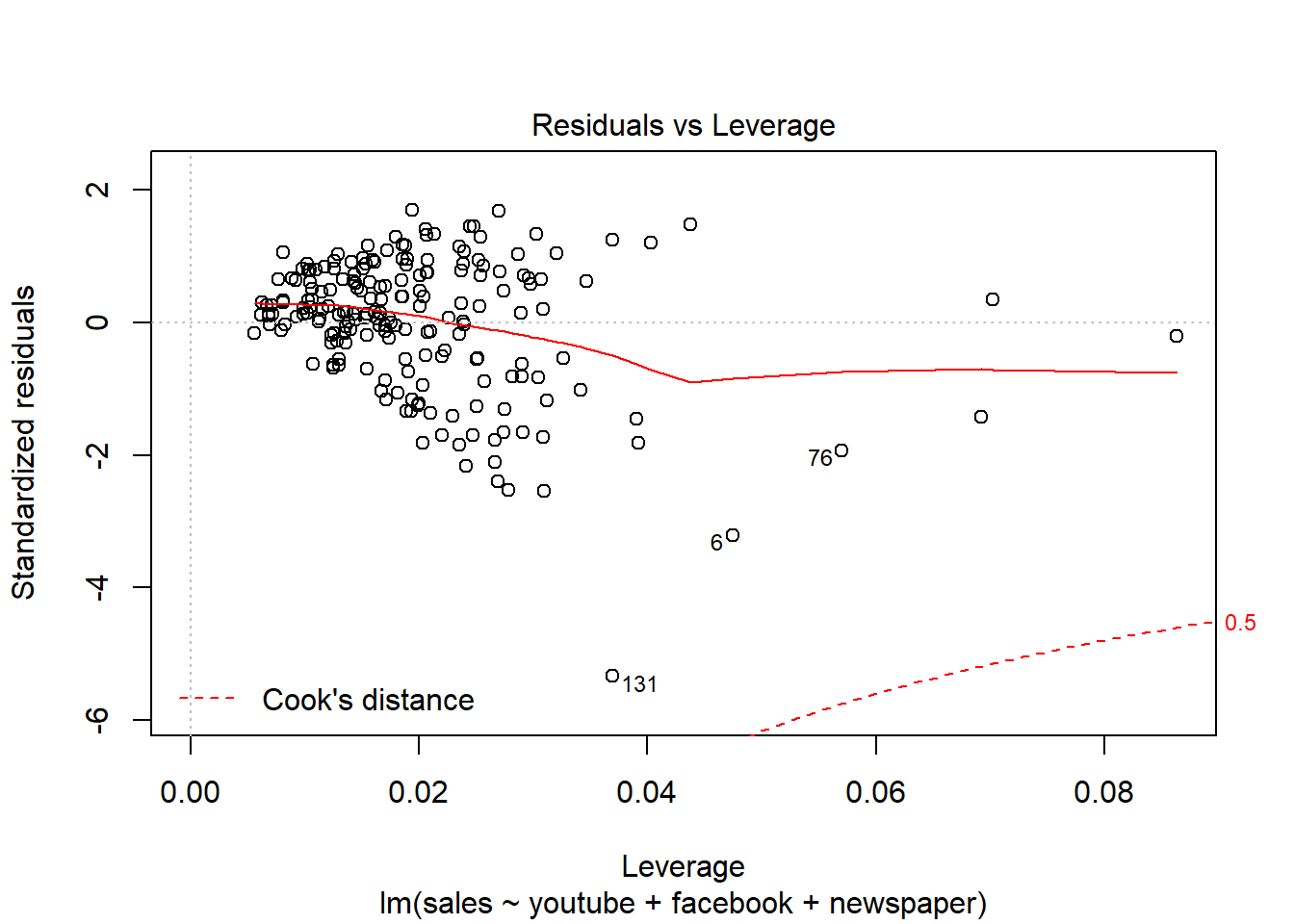
Wykres pokazuje jednorodność wariancji. Cel: linia ciągła jest pozioma, punkty równomiernie rozłożone, brak linii przerywanej. Dokładniejsze wytłumaczenie: link.
Ćwiczenia
- Wygeneruj w R idealny rozkład zgodny z liniową regresją wielokrotną np. za pomocą kod:
n <- 1000
x1 <- runif(n, min = 0, max = 100)
x2 <- runif(n, min = 0, max = 100)
y.good <- 5 + 0.2 * x1+14*x2 + rnorm(n, sd = 3)Przetestuj model i przeanalizuj wykresy.
- Przetestuj błędny model np.
y.bad<-5+sin(x1)+x2*x2+rnorm(n,sd=4)- Przeanalizuj wykresy dla ramek danych ze wcześniejszych ćwiczeń.