37  Matplotlib - inne wykresy

37.1 Wykres dwuosiowy

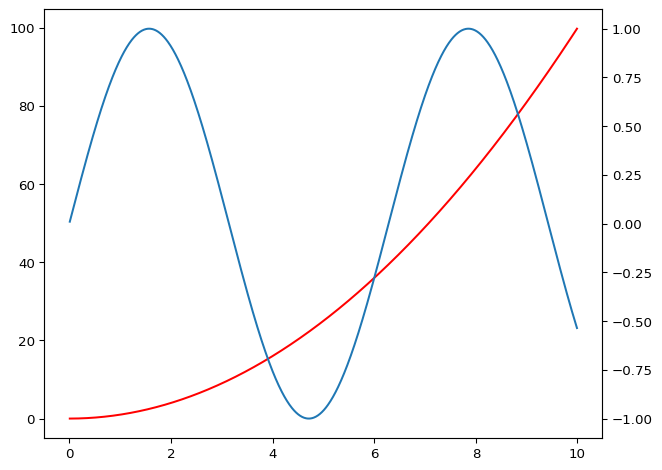
Funkcja twinx w bibliotece Matplotlib pozwala na utworzenie drugiej osi Y, która będzie współdzielić oś X z pierwszą osią Y. Dzięki temu, można w prosty sposób przedstawić dwie serie danych, które są mierzne w różnych jednostkach, ale mają wspólną zmienną niezależną.

Składnia funkcji to twinx(ax=None, **kwargs), gdzie:

• ax - obiekt Axes, który ma być użyty do tworzenia nowej osi Y. Domyślnie ustawione na None, co oznacza, że będzie tworzona nowa osie Y.
• **kwargs - dodatkowe argumenty dotyczące formatowania nowej osi Y.

import numpy as np
import matplotlib.pyplot as plt

fig, ax1 = plt.subplots()
x = np.arange(0.01, 10.0, 0.01)
y = x ** 2
ax1.plot(x, y, 'r')
ax2 = ax1.twinx()
y2 = np.sin(x)
ax2.plot(x, y2)
fig.tight_layout()
plt.show(block=True)

import numpy as np
import matplotlib.pyplot as plt

fig, ax1 = plt.subplots()
t = np.arange(0.01, 10.0, 0.01)
s1 = np.exp(t)
ax1.plot(t, s1, 'b-')
ax1.set_xlabel('time (s)')

ax1.set_ylabel('exp', color='b')
ax1.tick_params('y', colors='b')

ax2 = ax1.twinx()
s2 = np.sin(2 * np.pi * t)
ax2.plot(t, s2, 'r.')
ax2.set_ylabel('sin', color='r')
ax2.tick_params('y', colors='r')

fig.tight_layout()
plt.show(block=True)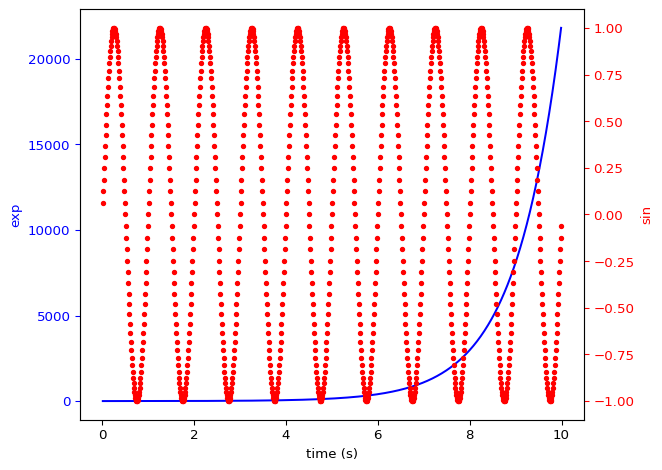

37.2 Wykres pudełkowy

Wykres pudełkowy (inaczej box plot) jest stosowany do przedstawiania informacji o rozkładzie danych liczbowych oraz do identyfikacji wartości odstających. Jest szczególnie przydatny w przypadku analizy danych ciągłych, które mają różne wartości i rozkłady. Oto kilka typów danych, dla których wykres pudełkowy może być stosowany:

1. Porównanie grup: Wykres pudełkowy jest używany do porównywania rozkładu danych między różnymi grupami. Na przykład, można go użyć do porównania wyników testów uczniów z różnych szkół, wynagrodzeń w różnych sektorach czy wartości sprzedaży różnych produktów.

2. Identyfikacja wartości odstających: Wykres pudełkowy jest używany do identyfikacji wartości odstających (outlierów) w danych, które mogą wskazywać na błędy pomiarowe, nietypowe obserwacje lub wartości ekstremalne. Na przykład, może to być użyte do wykrywania anomalii w danych meteorologicznych, wartościach giełdowych czy danych medycznych.

3. Analiza rozkładu: Wykres pudełkowy pomaga zrozumieć rozkład danych, takich jak mediana, kwartyle, zakres wartości i potencjalne wartości odstające. Może to być użyte w analizie danych takich jak oceny, wzrost ludności, wartość akcji czy ceny nieruchomości.

4. Wizualizacja wielowymiarowych danych: Wykres pudełkowy może być używany do wizualizacji wielowymiarowych danych, przedstawiając rozkład wielu zmiennych na jednym wykresie. Na przykład, można porównać zmienne takie jak wiek, zarobki i wykształcenie w badaniu demograficznym.

Warto zauważyć, że wykres pudełkowy jest szczególnie przydatny, gdy chcemy zrozumieć rozkład danych, ale nie pokazuje on konkretnej liczby obserwacji ani wartości indywidualnych punktów danych. W takich przypadkach inne rodzaje wykresów, takie jak wykres punktowy, mogą być bardziej odpowiednie.

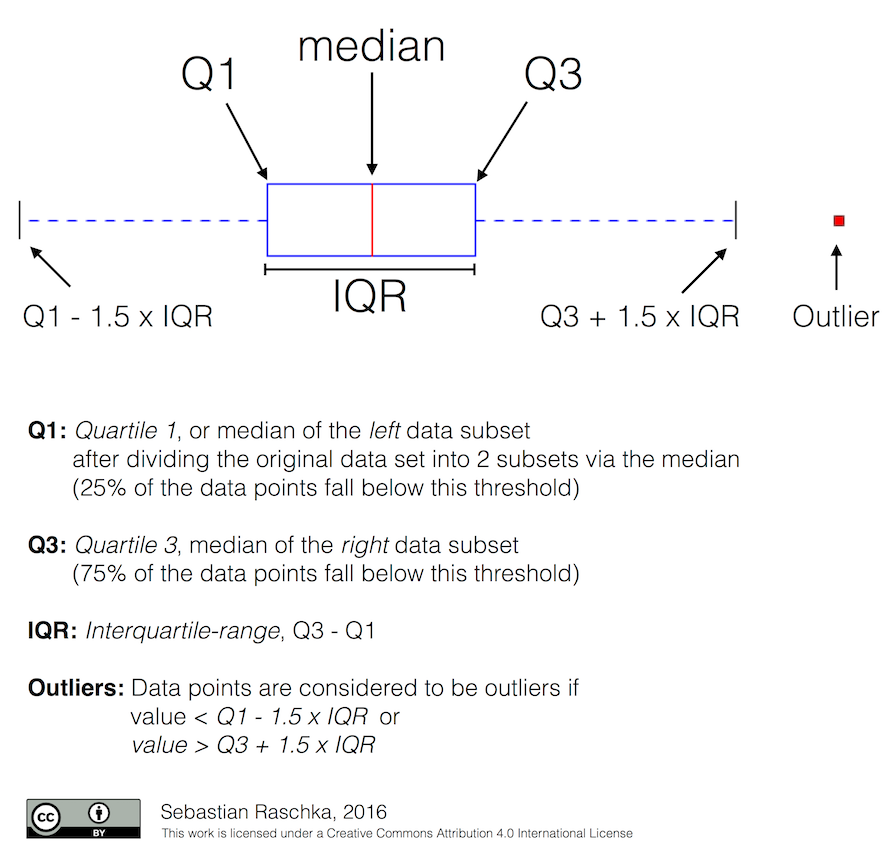
Wykres pudełkowy pokazuje pięć statystyk opisowych danych: minimum, pierwszy kwartyl (Q1), medianę, trzeci kwartyl (Q3) i maksimum.

import matplotlib.pyplot as plt
import numpy as np

# Przykładowe dane
data = np.random.rand(100)

# Tworzenie wykresu
fig, ax = plt.subplots()

# Rysowanie boxplota
ax.boxplot(data)

# Dodanie opisów
ax.set_title('Boxplot')
ax.set_ylabel('Wartości')
ax.set_xticklabels(['Przykładowe dane'])

# Wyświetlanie wykresu
plt.show(block=True)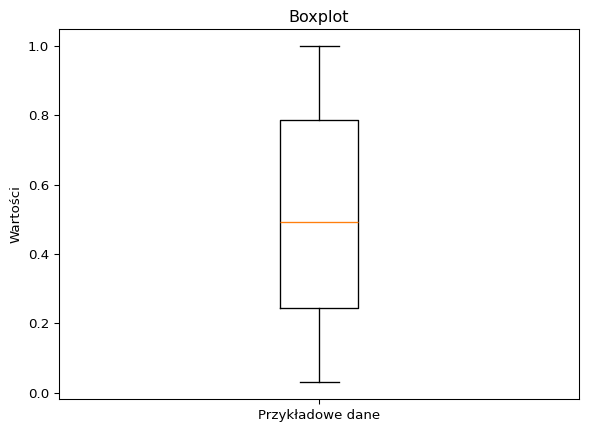

import matplotlib.pyplot as plt
import numpy as np

# Creating dataset
np.random.seed(10)
data = np.random.normal(100, 20, 200)

# Creating plot
plt.boxplot(data)

# show plot
plt.show(block=True)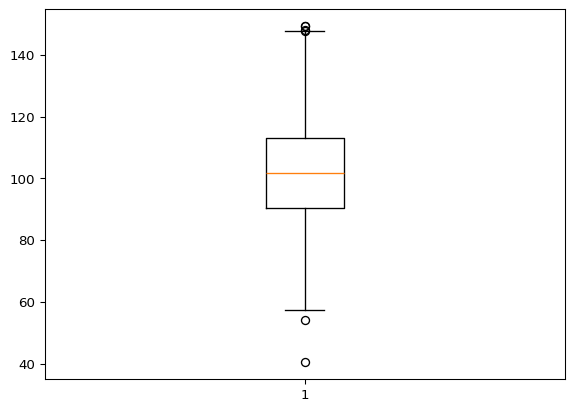

patch_artist=True, # kolorowe pudełka – włącza użycie obiektów typu „Patch” do rysowania samych pudełek, dzięki czemu możemy je wypełnić kolorem (sterowanym dalej przez boxprops).

notch=True, # wcięcia przy medianie – rysuje wcięcie („notch”) wokół linii mediany, co pomaga wizualnie ocenić istotność różnic między mediami.

boxprops=dict(facecolor='lightblue', edgecolor='navy'), – stylowanie samych pudełek:

• facecolor='lightblue' – wypełnienie pudełka jasnoniebieskim kolorem,
• edgecolor='navy' – obramowanie pudełka ciemnogranatowym.

medianprops=dict(color='darkred'), – właściwości linii mediany: jedynie kolor ciemnoczerwony (darkred).

whiskerprops=dict(color='navy'), – styl wąsów (ang. whiskers): kolor „navy” dla linii, które łączą pudełko z końcami zakresu danych (bez uwzględniania odstających).

capprops=dict(color='navy'), – styl „czapeczek” (caps) na końcach wąsów: również granatowy kolor.

flierprops=dict( – styl punktów odstających („fliers”, wartości poza zasięgiem whiskers):

* `marker='o'` – kółko jako znacznik,
* `markerfacecolor='gray'` – szare wypełnienie kółka,
* `markersize=5` – rozmiar znacznika,
* `linestyle='none'` – bez linii łączącej te punkty.

import pandas as pd
import matplotlib.pyplot as plt

# Przygotowanie danych
dane = pd.DataFrame({
    'Środek transportu': [
        'Samochód', 'Samochód', 'Samochód', 'Samochód', 'Samochód',
        'Rower',    'Rower',    'Rower',    'Rower',    'Rower',
        'Komunikacja miejska', 'Komunikacja miejska', 'Komunikacja miejska', 'Komunikacja miejska', 'Komunikacja miejska'
    ],
    'Czas dojazdu (minuty)': [
        25, 30, 28, 55, 32,
        20, 18, 22, 19, 21,
        40, 45, 42, 38, 44
    ]
})

# Przygotowanie danych do wykresu pudełkowego
grupy = dane['Środek transportu'].unique()
lista_czasow = [dane.loc[dane['Środek transportu'] == s, 'Czas dojazdu (minuty)']
                for s in grupy]

# Rysowanie wykresu
plt.figure(figsize=(8, 6))
plt.boxplot(
    lista_czasow,
    tick_labels=grupy,
    patch_artist=True,    # kolorowe pudełka
    notch=True,           # wcięcia przy medianie
    boxprops=dict(facecolor='lightblue', edgecolor='navy'),
    medianprops=dict(color='darkred'),
    whiskerprops=dict(color='navy'),
    capprops=dict(color='navy'),
    flierprops=dict(marker='o', markerfacecolor='gray', markersize=5, linestyle='none')
)

# Opisy osi i tytuł
plt.ylabel('Czas dojazdu [minuty]', fontsize=12)
plt.title('Porównanie czasów dojazdu do pracy\nw zależności od środka transportu', fontsize=14)

# Siatka i estetyka
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.tight_layout()

# Wyświetlenie
plt.show()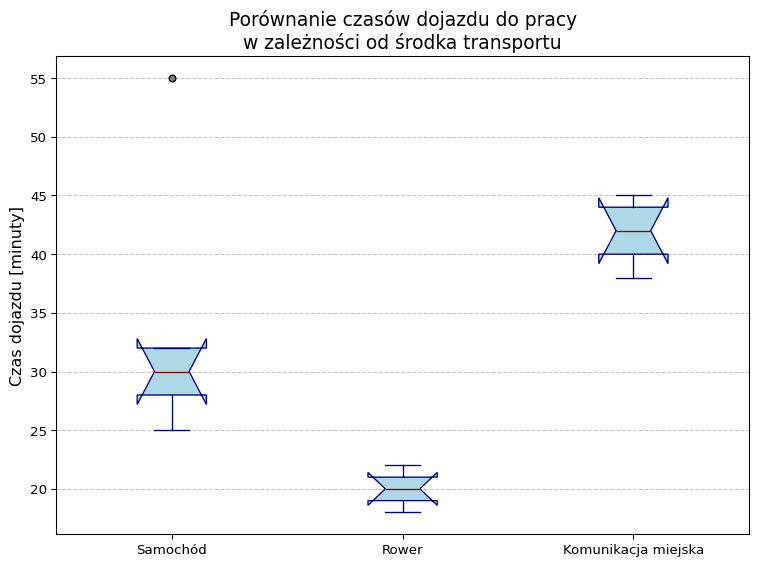

37.3 Histogram

Wykres histogramu jest stosowany do przedstawiania rozkładu danych liczbowych, zarówno ciągłych, jak i dyskretnych. Histogram pokazuje częstość występowania danych w określonych przedziałach (binach), co pozwala na analizę dystrybucji i identyfikację wzorców. Oto kilka typów danych, dla których histogram może być stosowany:

1. Analiza rozkładu: Histogram może być używany do analizy rozkładu danych, takich jak oceny, ceny, wartości akcji, wzrost ludności czy dane meteorologiczne. Pozwala to zrozumieć, jak dane są rozłożone, czy są skoncentrowane wokół pewnych wartości, czy mają długi ogon (tj. czy występują wartości odstające).

2. Identyfikacja tendencji: Histogram może pomóc w identyfikacji tendencji lub wzorców w danych. Na przykład, można użyć histogramu do identyfikacji sezonowych wzorców sprzedaży, zmian w wartościach giełdowych czy wzorców migracji ludności.

3. Porównanie grup: Histogram może być również używany do porównywania rozkładu danych między różnymi grupami. Na przykład, można go użyć do porównania wyników testów uczniów z różnych szkół, wynagrodzeń w różnych sektorach czy wartości sprzedaży różnych produktów.

4. Szacowanie parametrów: Histogram może pomóc w szacowaniu parametrów rozkładu, takich jak średnia, mediana czy wariancja, co może być użyteczne w analizie statystycznej.

Warto zauważyć, że histogram jest odpowiedni dla danych liczbowych, ale nie jest przeznaczony do przedstawiania danych kategorialnych. W takich przypadkach inne rodzaje wykresów, takie jak wykres słupkowy, mogą być bardziej odpowiednie.

import matplotlib.pyplot as plt

x = [1, 1, 2, 3, 3, 5, 7, 8, 9, 10,
     10, 11, 11, 13, 13, 15, 16, 17, 18, 18]

plt.hist(x, bins=4)
plt.show(block=True)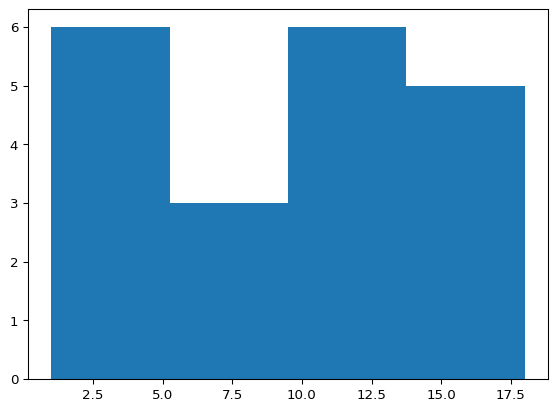

import pandas as pd
import matplotlib.pyplot as plt

ages = [20, 22, 25, 27, 21, 23, 37, 31, 61, 45, 41, 32]
bins = [18, 25, 35, 60, 100]
cats2 = pd.cut(ages, [18, 26, 36, 61, 100], right=False)
print(cats2)
group_names = ['Youth', 'YoungAdult',
               'MiddleAged', 'Senior']
data = pd.cut(ages, bins, labels=group_names)
plt.hist(data)
plt.show(block=True)

[[18, 26), [18, 26), [18, 26), [26, 36), [18, 26), ..., [26, 36), [61, 100), [36, 61), [36, 61), [26, 36)]
Length: 12
Categories (4, interval[int64, left]): [[18, 26) < [26, 36) < [36, 61) < [61, 100)]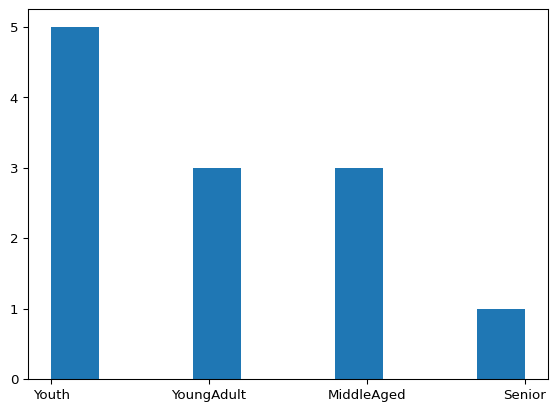

import matplotlib.pyplot as plt

ages = [20, 22, 25, 27, 21, 23, 37, 31, 61, 45, 41, 32]
bins = [18, 25, 35, 60, 100]
plt.hist(ages, bins=bins)
plt.show(block=True)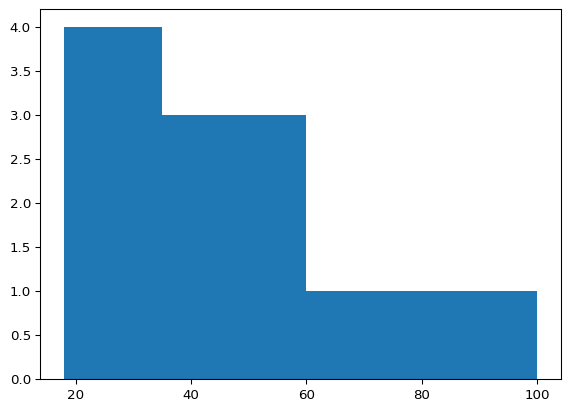

import matplotlib.pyplot as plt

x = [1, 1, 2, 3, 3, 5, 7, 8, 9, 10,
     10, 11, 11, 13, 13, 15, 14, 12, 18, 18]

plt.hist(x, bins=[0, 5, 10, 15, 20])
plt.xticks([0, 5, 10, 15, 20])
plt.show(block=True)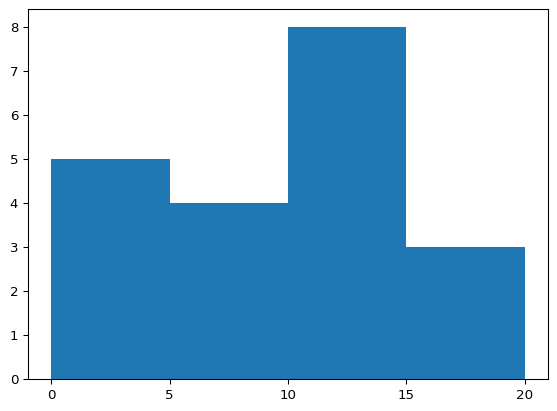

import matplotlib.pyplot as plt

x = [1, 1, 2, 3, 3, 5, 7, 8, 9, 10,
     10, 11, 11, 13, 13, 15, 14, 12, 18, 18]

plt.hist(x, bins=[0, 5, 10, 15, 20], cumulative=True)
plt.xticks([0, 5, 10, 15, 20])
plt.show(block=True)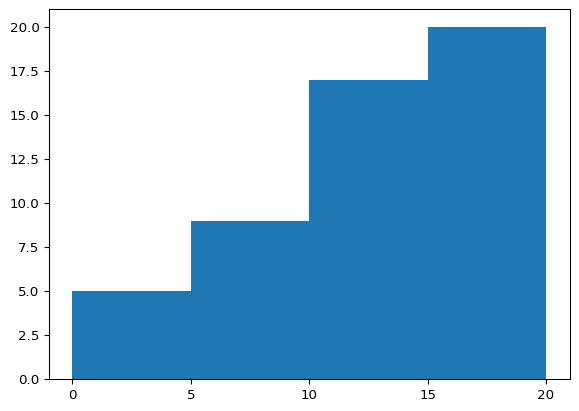

import matplotlib.pyplot as plt

x = [1, 1, 2, 3, 3, 5, 7, 8, 9, 10,
     10, 11, 11, 13, 13, 15, 14, 12, 18, 18]

plt.hist(x, bins=[0, 5, 10, 15, 20], density=True)
plt.xticks([0, 5, 10, 15, 20])
plt.show(block=True)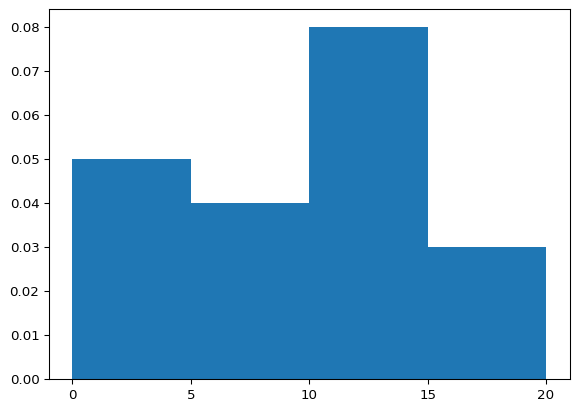

import pandas as pd
import matplotlib.pyplot as plt

# 1. Tworzymy ramkę danych
dane = pd.DataFrame({
    'Dzień': list(range(1, 17)),
    'Czas dojazdu (min)': [25, 30, 20, 35, 40, 22, 28, 33,
                           27, 32, 29, 31, 26, 24, 34, 36]
})

# 2. Rysujemy histogram
plt.figure(figsize=(8, 6))

plt.hist(
    dane['Czas dojazdu (min)'],
    bins=8,                    # liczba słupków
    edgecolor='black',         # obramowanie słupków
    alpha=0.7                  # przezroczystość dla lepszej estetyki
)

# 3. Oznaczenia i estetyka
plt.title('Histogram czasu dojazdu do pracy')
plt.xlabel('Czas dojazdu (minuty)')
plt.ylabel('Liczba dni')
plt.xticks(range(20, 45, 5))  # dostosowane podziałki na osi X
plt.grid(axis='y', alpha=0.75)

plt.tight_layout()
plt.show()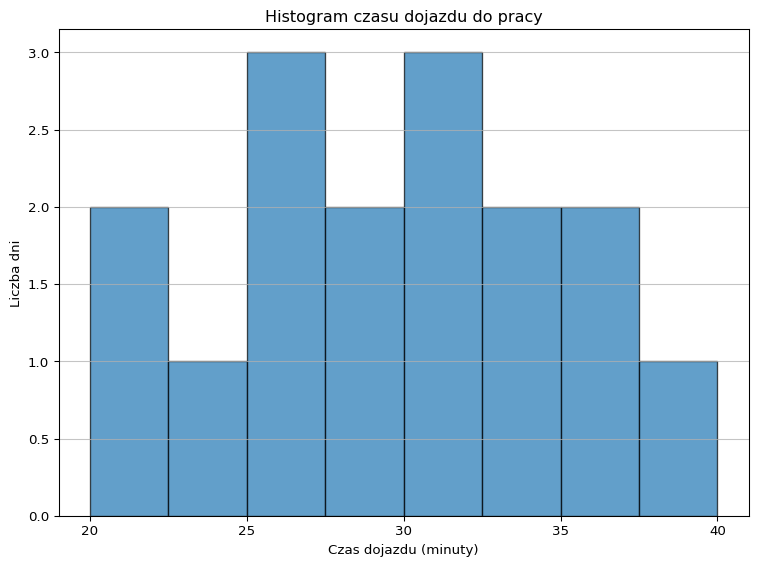

import pandas as pd
import matplotlib.pyplot as plt

# 1. Ramka danych
dane = pd.DataFrame({
    'Dzień': list(range(1, 15)),
    'Ilość kaw dziennie': [1, 2, 3, 3, 2, 4, 5, 3, 2, 1, 4, 3, 2, 3]
})

# 2. Rysujemy histogram z nowymi argumentami:
plt.figure(figsize=(8, 6))

plt.hist(
    dane['Ilość kaw dziennie'],
    bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5],  # precyzyjne przedziały wokół wartości 1–5
    color='lightblue',                     # kolor słupka
    edgecolor='black',                    # obramowanie każdego słupka
    alpha=0.7                             # przezroczystość
)

# 3. Podpisy i estetyka
plt.title('Histogram: liczba kaw wypitych dziennie')
plt.xlabel('Ilość kaw')
plt.ylabel('Liczba dni')
plt.xticks(range(1, 6))                  # od 1 do 5 kaw
plt.grid(axis='y', linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()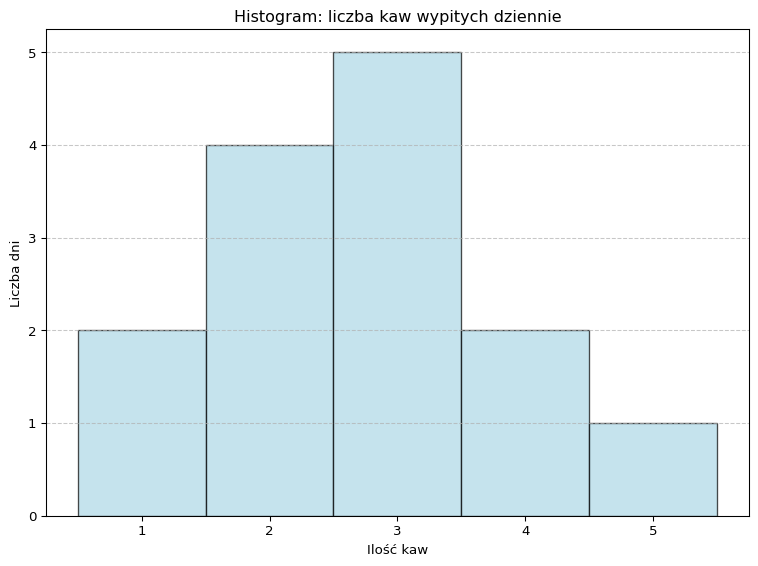

37.4 Wykresy w przestrzeni

37.4.1 Helisa

\[\begin{cases} x=a\cos (t) \\ y=a\sin(t) \\ z=at \end{cases}\]

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = plt.axes(projection='3d')
t = np.linspace(0, 15, 1000)
a = 3
xline = a * np.sin(t)
yline = a * np.cos(t)
zline = a * t
ax.plot3D(xline, yline, zline)
plt.show(block=True)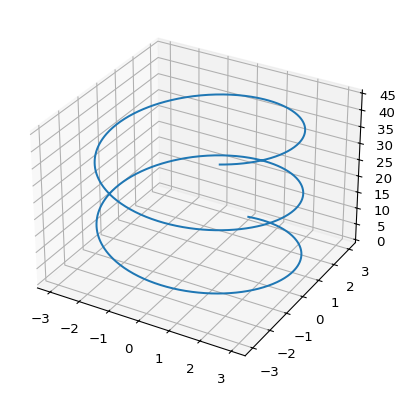

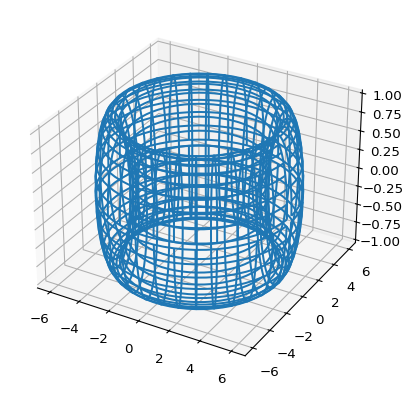
37.4.2 Torus

\[p(\alpha,\ \beta)=\Big((R+r\cos \alpha)\cos \beta,\ (R+r\cos \alpha)\sin \beta,\ r\sin \alpha\Big)\]

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = plt.axes(projection='3d')
r = 1
R = 5
alpha = np.arange(0, 2 * np.pi, 0.1)
beta = np.arange(0, 2 * np.pi, 0.1)
alpha, beta = np.meshgrid(alpha, beta)
x = (R + r * np.cos(alpha)) * np.cos(beta)
y = (R + r * np.cos(alpha)) * np.sin(beta)
z = r * np.sin(alpha)
ax.plot_wireframe(x, y, z)
plt.show(block=True)