10 Broadcasting

Rozważane warianty są przykładowe.

Wariant 1 - skalar-tablica - wykonanie operacji na każdym elemencie tablicy

import numpy as np

a = np.array([[1, 2], [5, 6], [9, 10]])
b = a + 4
print(b)
c = 2 ** a
print(c)

[[ 5  6]
 [ 9 10]
 [13 14]]
[[   2    4]
 [  32   64]
 [ 512 1024]]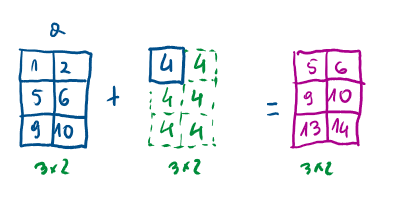

Wariant 2 - dwie tablice - “gdy jedna z tablic może być rozszerzona” (oba wymiary są równe lub jeden z nich jest równy 1)

https://numpy.org/doc/stable/user/basics.broadcasting.html

import numpy as np

a = np.array([[1, 2], [5, 6]])
b = np.array([9, 2])
r1 = a + b
print(r1)
r2 = a / b
print(r2)
c = np.array([[4], [-2]])
r3 = a + c
print(r3)
r4 = c / a
print(r4)

[[10  4]
 [14  8]]
[[0.11111111 1.        ]
 [0.55555556 3.        ]]
[[5 6]
 [3 4]]
[[ 4.          2.        ]
 [-0.4        -0.33333333]]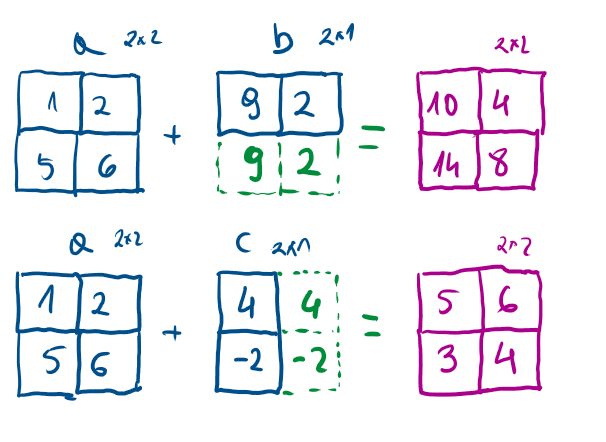

Wariant 3 - “kolumna” i “wiersz”

import numpy as np

a = np.array([[5, 2, -3]]).T
b = np.array([3, -2, 1, 2, 4])
print(a+b)
print(b+a)
print(a*b)

[[ 8  3  6  7  9]
 [ 5  0  3  4  6]
 [ 0 -5 -2 -1  1]]
[[ 8  3  6  7  9]
 [ 5  0  3  4  6]
 [ 0 -5 -2 -1  1]]
[[ 15 -10   5  10  20]
 [  6  -4   2   4   8]
 [ -9   6  -3  -6 -12]]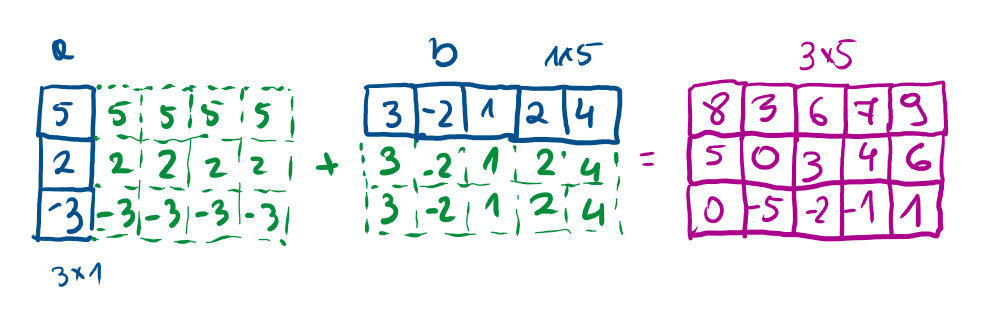

Ćwiczenia: (ex6.py)

Rozważ jednowymiarową tablicę
\[A = \begin{bmatrix}1 & 2 & 3\end{bmatrix}\]
oraz skalar \(k = 10\).
Wykonaj dodawanie, odejmowanie, mnożenie i dzielenie każdego elementu tablicy \(A\) przez \(k\) z wykorzystaniem broadcastingu.
Dla dwóch tablic jednowymiarowych
\[B_1 = \begin{bmatrix}1 & 2 & 3\end{bmatrix}, \quad B_2 = \begin{bmatrix}4 & 5 & 6\end{bmatrix},\]
wykonaj działanie \(B_1 + B_2\), \(B_1 - B_2\), \(B_1 * B_2\) oraz \(B_1 / B_2\) używając broadcastingu.
Mając dwie tablice dwuwymiarowe:
\[C_1 = \begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}, \quad C_2 = \begin{bmatrix}10 & 20 \\ 30 & 40\end{bmatrix},\]
dodaj je i odejmij od siebie, sprawdzając czy broadcasting zajdzie automatycznie.
Rozważ tablicę dwuwymiarową
\[D = \begin{bmatrix}1 & 2 & 3 \\ 4 & 5 & 6\end{bmatrix}\]
oraz wektor
\[v = \begin{bmatrix}10 & 100 & 1000\end{bmatrix}.\]
Wykonaj mnożenie i dzielenie elementowe tablicy \(D\) przez \(v\) z wykorzystaniem broadcastingu.
Dla tablicy
\[E = \begin{bmatrix}2 & 4 & 6 \\ 8 & 10 & 12\end{bmatrix}\]
podnieś każdy element do kwadratu, a następnie podziel przez wektor
\[w = \begin{bmatrix}2 & 2 & 2\end{bmatrix}\]
korzystając z broadcastingu.
Mając tablicę dwuwymiarową
\[F = \begin{bmatrix}1 & 2 \\ 3 & 4 \\ 5 & 6\end{bmatrix},\]
oraz skalar \(s = 2\), wykonaj \(F * s\), a następnie \(F^{s}\) (podnieś każdy element do potęgi \(s\)) z zastosowaniem broadcastingu.
Rozważ tablicę
\[G = \begin{bmatrix}10 & 20 & 30\end{bmatrix}\]
oraz kolumnową tablicę dwuwymiarową
\[h = \begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}.\] Dodaj do \(h\) tablicę \(G\) i zaobserwuj wynik broadcastingu.
Mając dwie tablice dwuwymiarowe o różnych wymiarach:
\[H_1 = \begin{bmatrix}1 & 2 & 3\end{bmatrix}, \quad H_2 = \begin{bmatrix}10 \\ 20 \\ 30\end{bmatrix},\]
spróbuj je dodać i pomnożyć przez siebie, korzystając z broadcastingu.
Rozważ tablicę dwuwymiarową
\[J = \begin{bmatrix}1 & 2 & 3 \\ 4 & 5 & 6\end{bmatrix}\]
oraz skalar \(m = 5\).
Wykonaj kombinację działań: najpierw pomnóż \(J\) przez \(m\), następnie odejmij \(m\), a na końcu podziel wynik przez \(m\) – wszystko z wykorzystaniem broadcastingu.