26 Matplotlib - wykres liniowy

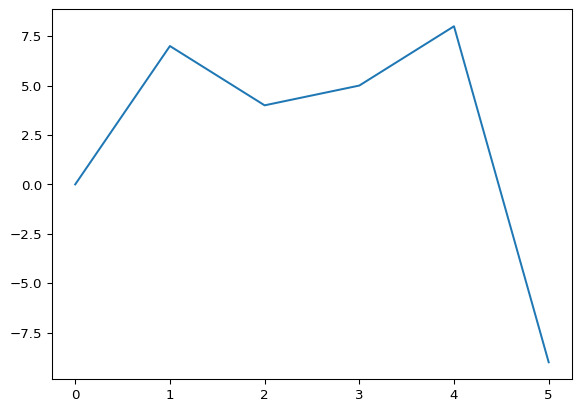
Wykres liniowy to jedno z najpotężniejszych narzędzi wizualizacji danych, które pozwala nam dostrzec zależności i trendy, które mogłyby pozostać niezauważone w surowych danych. Poniżej przedstawiam szczegółowe objaśnienie, kiedy i dlaczego warto sięgnąć po ten typ wykresu.

Wykres liniowy najlepiej sprawdza się, gdy chcemy przedstawić zmiany wartości w czasie lub w funkcji innej zmiennej ciągłej. Jego siła tkwi w zdolności do ukazywania ciągłych relacji między punktami danych, co pozwala na łatwe śledzenie trendów i wzorców.

Analiza zmian w czasie

Wykres liniowy doskonale obrazuje, jak dane zmieniają się w kolejnych jednostkach czasu. Jest nieoceniony przy prezentacji: - Trendów gospodarczych (wzrost PKB, inflacja, stopy bezrobocia) - Zmian na rynkach finansowych (kursy walut, ceny akcji, stopy procentowe) - Danych klimatycznych i pogodowych (zmiany temperatury, opady, poziom zanieczyszczeń) - Wskaźników zdrowotnych (tętno, poziom cukru we krwi, ciśnienie)

Ukazywanie zależności między zmiennymi

Gdy chcemy zbadać, jak jedna zmienna wpływa na drugą, wykres liniowy pozwala na intuicyjne przedstawienie tych relacji: - Związek między poziomem wykształcenia a średnimi zarobkami - Korelacja między wiekiem a określonymi umiejętnościami - Zależność między nakładami na reklamę a wynikami sprzedaży

Porównywanie wielu trendów jednocześnie

Wykres liniowy umożliwia efektywne zestawienie kilku serii danych na jednym wykresie: - Analiza sprzedaży różnych produktów w czasie - Porównanie wyników różnych regionów, zespołów lub krajów - Zestawienie faktycznych wyników z planowanymi celami - Porównanie różnych wskaźników ekonomicznych w tym samym okresie

Analiza korelacji i przyczynowości

Linie na wykresie pomagają dostrzec, jak zmiany jednej zmiennej mogą wpływać na inne: - Badanie wpływu cen paliwa na sprzedaż różnych typów pojazdów - Analiza związku między temperaturą otoczenia a zużyciem energii - Ocena wpływu kampanii marketingowych na świadomość marki

Identyfikacja anomalii i punktów zwrotnych

Wykres liniowy pozwala szybko zauważyć wartości odstające oraz momenty znaczących zmian: - Wykrywanie nietypowych wzorców w danych finansowych - Identyfikacja punktów przełomowych w trendach społecznych - Rozpoznawanie sezonowych wahań w danych

Choć wykresy liniowe są najodpowiedniejsze dla danych ciągłych, mogą być również wykorzystywane do prezentacji danych dyskretnych, o ile istnieje logiczny związek między kolejnymi punktami. Na przykład, miesięczne wyniki sprzedaży to dane dyskretne, ale ich przedstawienie w formie linii pomoże dostrzec trend roczny.

Należy jednak pamiętać, że łączenie punktów linią sugeruje ciągłość między nimi. Jeśli nie ma logicznej ciągłości między punktami danych (np. przy porównywaniu niezwiązanych ze sobą kategorii), lepszym wyborem będzie wykres słupkowy lub punktowy.

import matplotlib.pyplot as plt

x = [0, 7, 4, 5, 8, -9]
plt.plot(x)
plt.show()

import matplotlib.pyplot as plt
import numpy as np

1x = np.linspace(0, 2, 100)
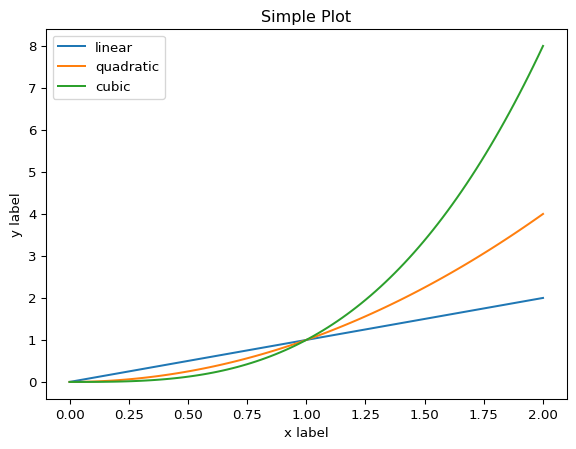
2plt.plot(x, x, label='linear')
3plt.plot(x, x ** 2, label='quadratic')
4plt.plot(x, x ** 3, label='cubic')
5plt.xlabel('x label')
6plt.ylabel('y label')
7plt.title("Simple Plot")
8plt.legend()
9plt.show()

1: x = np.linspace(0, 2, 100): tworzy tablicę x z 100 równomiernie rozłożonymi wartościami od 0 do 2 (włącznie), korzystając z funkcji linspace z biblioteki numpy.
2: plt.plot(x, x, label='linear'): rysuje liniowy wykres (y = x) z wartościami z tablicy x.
3: plt.plot(x, x**2, label='quadratic'): rysuje wykres kwadratowy (y = x^2) z wartościami z tablicy x.
4: plt.plot(x, x**3, label='cubic'): rysuje wykres sześcienny (y = x^3) z wartościami z tablicy x.
5: plt.xlabel('x label'): dodaje etykietę osi X.
6: plt.ylabel('y label'): dodaje etykietę osi Y.
7: plt.title("Simple Plot"): nadaje tytuł wykresu “Simple Plot”.
8: plt.legend(): dodaje legendę do wykresu, która pokazuje etykiety (label) dla poszczególnych linii.
9: plt.show(): wyświetla wykres.

Wersja obiektowa:

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
x = np.linspace(0, 2, 100)

ax.plot(x, x, label='linear')
ax.plot(x, x ** 2, label='quadratic')
ax.plot(x, x ** 3, label='cubic')

ax.set_xlabel('x label')
ax.set_ylabel('y label')
ax.set_title("Simple Plot")

ax.legend()
plt.show()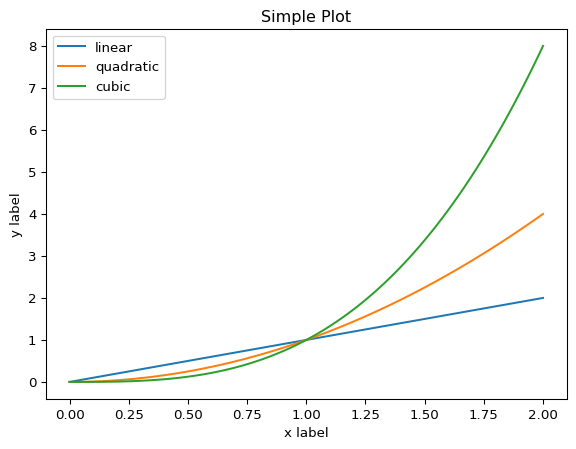

Wersja z datami:

import matplotlib.pyplot as plt
import numpy as np

daty = np.arange('2024-01', '2025-01', dtype='datetime64') 

index = np.arange(len(daty))

y_1 = index
y_2 = index ** 2
y_3 = index ** 3

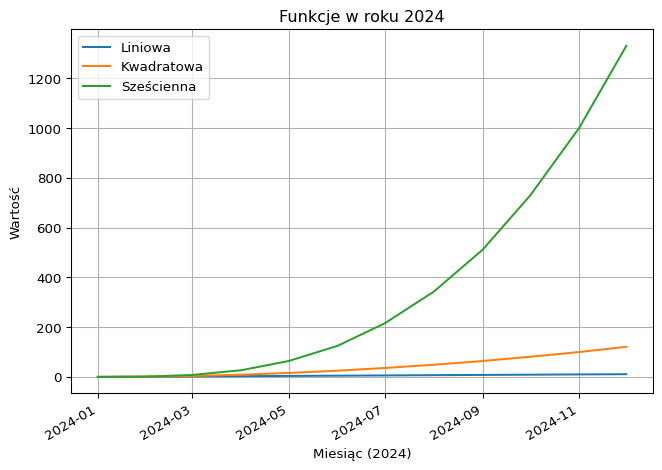
plt.plot(daty, y_1, label='Liniowa')
plt.plot(daty, y_2, label='Kwadratowa')
plt.plot(daty, y_3, label='Sześcienna')

plt.xlabel('Miesiąc (2024)')
plt.ylabel('Wartość')
plt.title("Funkcje w roku 2024")
plt.legend()
plt.grid(True)

plt.show()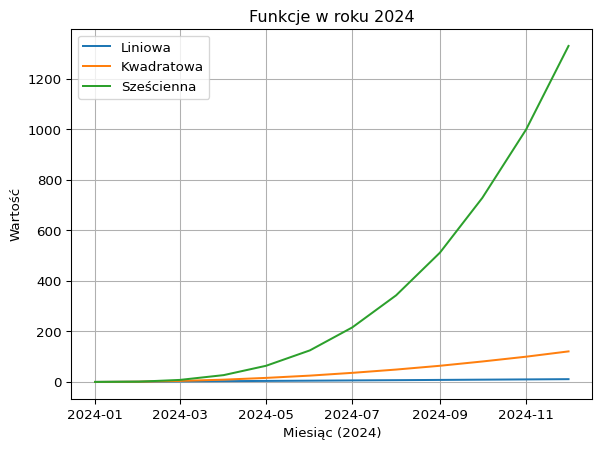

import matplotlib.pyplot as plt
import numpy as np

# Tworzenie danych
daty = np.arange('2024-01', '2025-01', dtype='datetime64')
index = np.arange(len(daty))
y_1 = index
y_2 = index**2
y_3 = index**3

# Tworzenie figury i osi w podejściu obiektowym
fig, ax = plt.subplots()

# Rysowanie linii na osiach
ax.plot(daty, y_1, label='Liniowa')
ax.plot(daty, y_2, label='Kwadratowa')
ax.plot(daty, y_3, label='Sześcienna')

# Dodawanie etykiet i tytułu
ax.set_xlabel('Miesiąc (2024)')
ax.set_ylabel('Wartość')
ax.set_title('Funkcje w roku 2024')

# Dodawanie legendy i siatki
ax.legend()
ax.grid(True)

# Dostosowanie wyglądu - opcjonalne ulepszenia
fig.autofmt_xdate()  # Automatyczne formatowanie dat na osi X dla lepszej czytelności
plt.tight_layout()   # Automatyczne dostosowanie rozmiaru wykresu

# Wyświetlenie wykresu
plt.show()