np.array - argumenty rzutowany na tablicę (coś po czym można iterować) - warto sprawdzić rozmiar/kształt
import numpy as np
tab = np.array([2, -3, 4])
print(tab)
print("size:", tab.size)
tab2 = np.array((4, -3, 3, 2))
print(tab2)
print("size:", tab2.size)
tab3 = np.array({3, 3, 2, 5, 2})
print(tab3)
print("size:", tab3.size)
tab4 = np.array({"pl": 344, "en": 22})
print(tab4)
print("size:", tab4.size)[ 2 -3 4]
size: 3
[ 4 -3 3 2]
size: 4
{2, 3, 5}
size: 1
{'pl': 344, 'en': 22}
size: 1np.zeros - tworzy tablicę wypełnioną zerami
import numpy as np
tab = np.zeros(4)
print(tab)
print(tab.shape)
tab2 = np.zeros([2, 3])
print(tab2)
print(tab2.shape)
tab3 = np.zeros([2, 3, 4])
print(tab3)
print(tab3.shape)[0. 0. 0. 0.]
(4,)
[[0. 0. 0.]
[0. 0. 0.]]
(2, 3)
[[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]]
(2, 3, 4)np.ones - tworzy tablicę wypełnioną jedynkami (to nie odpowiednik macierzy jednostkowej!)
import numpy as np
tab = np.ones(4)
print(tab)
print(tab.shape)
tab2 = np.ones([2, 3])
print(tab2)
print(tab2.shape)
tab3 = np.ones([2, 3, 4])
print(tab3)
print(tab3.shape)[1. 1. 1. 1.]
(4,)
[[1. 1. 1.]
[1. 1. 1.]]
(2, 3)
[[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]]
(2, 3, 4)np.diag - tworzy tablicę odpowiadającą macierzy diagonalnej
import numpy as np
print("tab0")
tab0 = np.diag([3, 4, 5])
print(tab0)
print("tab1")
tab1 = np.array([[2, 3, 4], [3, -4, 5], [3, 4, -5]])
print(tab1)
tab2 = np.diag(tab1)
print("tab2")
print(tab2)
tab3 = np.diag(tab1, k=1)
print("tab3")
print(tab3)
print("tab4")
tab4 = np.diag(tab1, k=-2)
print(tab4)
print("tab5")
tab5 = np.diag(np.diag(tab1))
print(tab5)tab0
[[3 0 0]
[0 4 0]
[0 0 5]]
tab1
[[ 2 3 4]
[ 3 -4 5]
[ 3 4 -5]]
tab2
[ 2 -4 -5]
tab3
[3 5]
tab4
[3]
tab5
[[ 2 0 0]
[ 0 -4 0]
[ 0 0 -5]]np.arange - tablica wypełniona równomiernymi wartościami
Składnia: numpy.arange([start, ]stop, [step, ]dtype=None)
Zasada działania jest podobna jak w funkcji range, ale dopuszczamy liczby “z ułamkiem”.
import numpy as np
a = np.arange(3)
print(a)
b = np.arange(3.0)
print(b)
c = np.arange(3, 7)
print(c)
d = np.arange(3, 11, 2)
print(d)
e = np.arange(0, 1, 0.1)
print(e)
f = np.arange(3, 11, 2, dtype=float)
print(f)
g = np.arange(3, 10, 2)
print(g)[0 1 2]
[0. 1. 2.]
[3 4 5 6]
[3 5 7 9]
[0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]
[3. 5. 7. 9.]
[3 5 7 9]np.linspace - tablica wypełniona równomiernymi wartościami wg skali liniowej
import numpy as np
a = np.linspace(2.0, 3.0, num=5)
print(a)
b = np.linspace(2.0, 3.0, num=5, endpoint=False)
print(b)
c = np.linspace(10, 20, num=4)
print(c)
d = np.linspace(10, 20, num=4, dtype=int)
print(d)[2. 2.25 2.5 2.75 3. ]
[2. 2.2 2.4 2.6 2.8]
[10. 13.33333333 16.66666667 20. ]
[10 13 16 20]
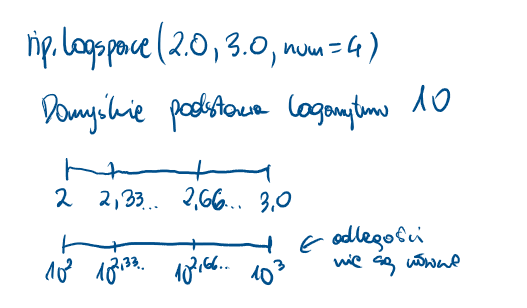
np.logspace - tablica wypełniona wartościami wg skali logarytmicznej
Składnia: numpy.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None, axis=0)
import numpy as np
a = np.logspace(2.0, 3.0, num=4)
print(a)
b = np.logspace(2.0, 3.0, num=4, endpoint=False)
print(b)
c = np.logspace(2.0, 3.0, num=4, base=2.0)
print(c)[ 100. 215.443469 464.15888336 1000. ]
[100. 177.827941 316.22776602 562.34132519]
[4. 5.0396842 6.34960421 8. ]
np.empty - pusta (niezaincjowana) tablica - konkretne wartości nie są “gwarantowane”
import numpy as np
a = np.empty(3)
print(a)
b = np.empty(3, dtype=int)
print(b)[0. 1. 2.]
[ 0 4607182418800017408 4611686018427387904]np.identity - tablica przypominająca macierz jednostkową
np.eye - tablica z jedynkami na przekątnej (pozostałe zera)
import numpy as np
print("a")
a = np.identity(4)
print(a)
print("b")
b = np.eye(4, k=1)
print(b)
print("c")
c = np.eye(4, k=2)
print(c)
print("d")
d = np.eye(4, k=-1)
print(d)a
[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
b
[[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]
[0. 0. 0. 0.]]
c
[[0. 0. 1. 0.]
[0. 0. 0. 1.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
d
[[0. 0. 0. 0.]
[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]]Ćwiczenia: (ex3.py)
Utwórz jednowymiarową tablicę zawierającą liczby całkowite od 1 do 5 i przypisz ją do zmiennej A. Wynikowa tablica powinna mieć postać: \[\begin{bmatrix}1 & 2 & 3 & 4 & 5\end{bmatrix} \]
Utwórz dwuwymiarową tablicę zawierającą elementy: \[\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix} \]
i przypisz ją do zmiennej B.
Utwórz tablicę zawierającą liczby od 0 do 9 (włącznie). Przypisz ją do zmiennej C.
Oczekiwana postać: \[\begin{bmatrix}0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9\end{bmatrix} \]
Utwórz tablicę zawierającą liczby od 10 do 30 z krokiem 5. Przypisz do D.
Oczekiwana postać: \[\begin{bmatrix}10 & 15 & 20 & 25 & 30\end{bmatrix} \]
Utwórz tablicę 5 wartości równomiernie rozłożonych pomiędzy 0 a 1. Przypisz do E.
Przykładowa postać: \[\begin{bmatrix}0. & 0.25 & 0.5 & 0.75 & 1.\end{bmatrix} \]
Utwórz dwuwymiarową tablicę o wymiarach 2x3 wypełnioną zerami. Przypisz do F.
Oczekiwana postać: \[\begin{bmatrix}0 & 0 & 0 \\ 0 & 0 & 0\end{bmatrix} \]
Korzystając z np.eye utwórz macierz jednostkową 4x4. Przypisz do J.
Oczekiwana postać: \[\begin{bmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix} \]